Francisco Gabriel Hernández Zamora*
¿Cuántas formas hay de llegar de tu casa a la escuela donde estudias? ¿Cuántas maneras hay de pintar una cuadrícula de tamaño 3×3 con tres colores distintos? Si las preguntas de este tipo suponen un reto para tu imaginación y te entusiasma intentar responderlas, seguramente te gustan las matemáticas, puesto que detrás de la solución se encuentran éstas. ¿Eres estudiante menor de 20 años y cursas el nivel de secundaria o bachillerato en el estado de Veracruz? De ser así, entonces puedes participar en los concursos de la Olimpiada Mexicana de Matemáticas (OMM) que se realizan anualmente en la entidad.
En nuestro país un grupo de profesores de la UNAM y el IPN tuvo la idea de difundir las matemáticas a través de concursos, surgiendo de esta manera la OMM, teniendo como sede de su primer Concurso Nacional la ciudad de Xalapa, Veracruz, en septiembre de 1987, año a partir del cual se ha realizado el evento anualmente. Así pues, la OMM surgió como un programa de la Sociedad Matemática Mexicana, cuyo objetivo es promover el estudio de las matemáticas en forma creativa, buscando desarrollar el razonamiento y la imaginación de los jóvenes.
El proceso de selección de la delegación de Veracruz, que nos representa en el Concurso Nacional en noviembre de cada año, comienza en febrero; esto a través de los sistemas y subsistemas de enseñanza básica y media superior del estado. Primeramente, en las escuelas se realiza la detección y selección de chicos con habilidades sobresalientes en matemáticas, estos chicos representan a sus escuelas en otras etapas como pueden ser exámenes de zona, regionales y estatales por sistema y subsistema, para llegar al Concurso Estatal en el mes de junio.
La preselección se conforma por los 18 estudiantes que obtengan la mayor puntuación en el Concurso Estatal, a quienes se les da un entrenamiento que tiene como objetivo su preparación para presentar el Examen Selectivo 1, que destaca a doce participantes, quienes reciben una preparación aún más rigurosa para presentar el Examen Selectivo 2, a través del cual se elige a seis estudiantes que finalmente integran la delegación que participa en el Concurso Nacional, representando al Estado de Veracruz. Cabe señalar que los exámenes que se aplican en las diversas etapas son todo un reto a la imaginación de los jóvenes, quienes con entusiasmo se adentran al maravilloso mundo de la abstracción inmerso en las matemáticas.
Participación destacada
Del 5 al 10 de noviembre de 2017 se llevó a cabo en Santiago, Nuevo León, el XXXI Concurso de la OMM. Durante esa semana se realizaron el examen, las sesiones de coordinación, las reuniones del jurado y la ceremonia de premiación, además de diversas actividades sociales y culturales para los participantes. El Comité Organizador de la OMM elaboró el examen a partir de los problemas que le envían las delegaciones estatales, así como miembros de la comunidad matemática del país. Los problemas elegidos versan sobre distintos temas de matemáticas básicas y deben ser inéditos.
El examen consta de dos pruebas escritas que se aplican en dos días consecutivos, cada una de las cuales consta de tres problemas y se otorgan cuatro horas y media para su resolución. Cada concursante presenta por escrito su solución para cada uno de los seis problemas. La resolución correcta de los problemas del examen requiere, en general, de mucho ingenio y de gran habilidad en el manejo de conocimientos básicos de matemáticas.
Cabe destacar que la participación por parte de la delegación de Veracruz en el XXXI Concurso de la OMM fue sobresaliente, obteniendo dos medallas de plata y una de bronce. Los estudiantes que nos representaron fueron: Carlos Reyes Valdivieso, Iván García Mestiza (plata), Mariola Camacho Lie (bronce), Yeudiel Lara Moreno (plata), Santiago Atilano Hernández y Francisco Javier Barragán Sánchez.
Dos problemas
Veamos un par de ejemplos de problemas que se trabajaron en el XXXI Concurso de la OMM:
Problema 1. En un salón hay 35 alumnos. El primer día de clase cada alumno es amigo de 17 de sus compañeros, al siguiente día cada alumno se hace amigo de los amigos de sus amigos y así cada día siguiente. ¿Será posible que eventualmente todos sean amigos? Justifica tu respuesta.
Solución: Nos fijamos en un niño P. El primer día el niño P tiene 17 amigos, de los 17 que no son sus amigos al menos hay uno que es amigo de un amigo de P, por lo tanto al segundo día hay al menos 18 amigos de P. Y quedan a lo más 16 que no son amigos de P, por lo que al tercer día al menos 19 son amigos de P. Como cada día queda al menos uno menos que aún no es amigo de P, es claro que en a lo más 17 días todos serán amigos de P. Por lo tanto eventualmente todos serán amigos.
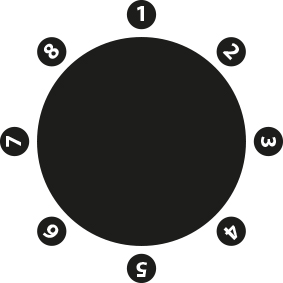
Problema 2. Ocho personas están sentadas alrededor de una mesa redonda, como se muestra en la Figura 1. Intercambian lugares una pareja a la vez. Sólo está permitido intercambiar lugares con el vecino de la izquierda o con el de la derecha. ¿Cuál es el menor número de intercambios que debe hacerse para que todos ocupen el lugar del compañero que tenían enfrente al comienzo del juego?
Solución: Primeramente observamos que para mover a una persona a la silla opuesta se necesitan al menos cuatro movimientos. Además, en cada movimiento se mueve a dos personas, por lo que al menos se necesitarán 16 movimientos para llevar a cada persona a la silla opuesta. Así que sólo necesitamos encontrar una manera de mover a todos al lugar opuesto en exactamente 16 movimientos.
Numeramos los lugares del 1 al 8 en sentido horario como se muestra en la Figura 2. Para llevar a la persona que está en la silla 1 a la silla 5 procedemos como sigue: intercambiamos a las personas que están en las sillas 1 y 2, luego a las que están en las sillas 2 y 3, luego a las que están en las sillas 3 y 4, y finalmente a las que están en las sillas 4 y 5.
A continuación, usando el procedimiento descrito en el párrafo anterior, llevamos a la persona que está en la silla 8 a la silla 4, a la persona que está en la silla 7 a la silla 3, y finalmente a la persona que está en la silla 6 a la silla 2. Es claro que las personas que faltan quedan acomodadas en la silla opuesta a la que estaban al principio y necesitamos exactamente 16 movimientos.
*Facultad de Matemáticas UV.
Correo: francischernandez@uv.mx
Edición: Eliseo Hernández Gutiérrez
Ilustración: Francisco J. Cobos Prior
Redes Sociales: Katya L. Zamora
Dir. de Comunicación de la Ciencia, UV
dcc@uv.mx
