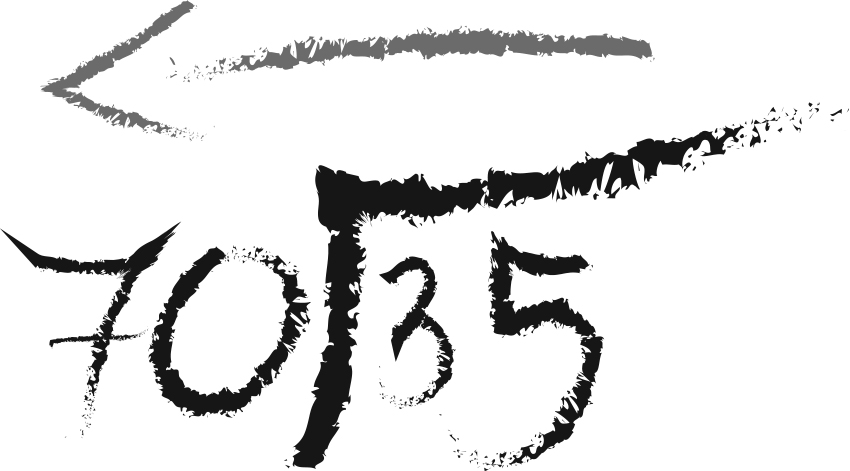Alfonso Javier Bustamante Santos*
Debido a los bajos puntajes que los estudiantes mexicanos han obtenido durante los últimos años en las pruebas estandarizadas internacionales como el Programa para la Evaluación Internacional de Estudiantes (PISA por sus siglas en inglés) y las nacionales como ENLACE (Evaluación Nacional de Logros en Centros Escolares) y EXCALE (Examen para la Calidad y el Logro Educativo), se ha mencionado en algunos medios que los mexicanos estamos reprobados en matemáticas o más específicamente en razonamiento matemático.
La palabra “reprobado” la podemos relacionar con otras palabras como fracaso o con algunas más desagradables. Por ejemplo, en el diccionario de la lengua española se define como “Condenado a penas eternas”. Ya podemos imaginar el estigma en una persona, o en una nación, cuando se les califica de este modo.
En el grupo que conforma la Línea de Investigación en Legua Escrita y Matemática Básica, de la Universidad Veracruzana, consideramos que los puntajes obtenidos se deben también a otros aspectos y no sólo al razonamiento de los estudiantes. Por ello nos propusimos hacer una serie de investigaciones sobre la manera en que los estudiantes de educación básica resuelven algunos problemas de matemáticas y de español.
Los resultados indican que la mayoría de estudiantes con bajos puntajes en estas pruebas también presenta carencias en servicios de transporte, comunicación, salud; sus padres tienen baja escolaridad, dificultades laborales, así como económicas. Consideramos entonces que el reprobar matemáticas también refleja las condiciones de vida de las familias en las que crecen nuestros estudiantes y no la falta de razonamiento o de inteligencia, como a veces se cree desde el sentido común.
En un estudio realizado para explorar en qué se equivocan los estudiantes cuando resuelven un problema matemático, se encontró que hay quienes no recuerdan cómo hacer las operaciones básicas (suma, resta, multiplicación y división). Algunos consideran que pueden dar un resultado aproximado, es decir, que no se requiere precisión y exactitud. Otros han comprendido parcialmente el sistema de numeración decimal y las unidades de longitud. Pero hay en particular algunos estudiantes que tuvieron dificultades con la “escritura” de las operaciones que realizaron y de sus resultados.
En este tema quiero profundizar, por lo que, estimada lectora o lector, por favor resuelva el siguiente problema en el recuadro. Escriba sus operaciones para que observe con claridad las dificultades que experimentan los estudiantes.
| Héctor camina 35 metros y da 70 pasos, ¿de qué tamaño son sus pasos? |
Como usted, algunos estudiantes también lo resolvieron por cálculo mental y escribieron el resultado de manera correcta (que no daremos aquí para no influenciar su respuesta). Otros escribieron operaciones, pero particularmente la división. Ellos dicen, por ejemplo: “Voy a dividir treinta y cinco entre setenta” y lo escriben en el orden en que lo dicen y de izquierda a derecha como lo hacemos cuando escribimos con letras.
Figura 1. Escritura de la división de izquierda a derecha.
Pero en esta división no hay correspondencia entre el orden en que se dicen y el orden en que se escriben los datos, por eso queda una división diferente: setenta entre treinta y cinco, como se muestra en la Figura 1. Si resolvemos esa división obtenemos 2, que es generalmente interpretado como 2 metros y por lo tanto es incorrecto.
¿Por qué sucede esto? Concluimos que los estudiantes, como todos nosotros, están más familiarizados con la escritura con letras (alfabética) que con la escritura de las matemáticas (notación matemática) y cada uno de estos sistemas tiene reglas y propiedades diferentes. Si las desconocemos entonces usamos lo que sí sabemos de un sistema y lo aplicamos en el otro, y eso, obviamente, provoca errores como el que ya vimos.
Pero vamos a suponer que los estudiantes tuvieron la oportunidad de reflexionar en clase sobre la escritura de las matemáticas y logran escribir la operación adecuadamente.
Figura 2. Representación gráfica de la división 35 entre 70.
Ahora hay que lidiar con el punto decimal. ¿En dónde se coloca? ¿Arriba del 3, del 5 ó entre ellos? Estas dudas expresan desconocimiento del sistema de numeración, de los números decimales y las reglas del algoritmo de la división. Estos temas son básicos y debemos dominarlos bien porque a partir de ellos podemos construir nuevos y más complejos conocimientos, pero si éstos no están bien cimentados, seguramente experimentaremos dificultades en su escritura y eso se reflejará también en los resultados de las famosas pruebas.
Para finalizar, quisiera enfatizar que, contrariamente a lo que muchos piensan, las matemáticas no son un lenguaje, sino un conocimiento construido por las personas al enfrentar múltiples situaciones de la vida diaria. El lenguaje matemático sólo es una parte de las matemáticas que se debe conocer, dominar y diferenciar de otros lenguajes para su uso adecuado.
Las matemáticas forman un conjunto de nociones, de relaciones, de sistemas de relaciones que se apoyan unos a otros, donde la escritura (la representación gráfica) es sólo una pequeña parte pero muy importante porque ayuda a reflexionar, a comunicar los resultados y por lo tanto al desarrollo de la matemática. Así, quienes pensaron en hacer una división para este problema aplicaron el razonamiento matemático adecuadamente e identificaron las relaciones correctas entre los datos (el 75% de los estudiantes que participaron en el estudio lo hicieron). Esto significa que sí razonan. Quienes no dieron la respuesta correcta (.5 metros, ½ metro, 50 cm. o sus equivalentes) posiblemente se deba a dificultades en la representación escrita de esos conocimientos. Ahí es donde entra el trabajo de los maestros, quienes con suficiente tiempo y en condiciones favorables de trabajo podrían apoyar a los estudiantes a comprender este sistema de representación a través de una didáctica específica, como la que se propone en español.
*Doctor en Investigación Educativa por la Universidad Veracruzana, Maestro en Ciencias en la especialidad en Investigaciones Educativas del DIE-CINVESTAV.
Dudas y comentarios: javierbtte@hotmail.com
Diseño: L.D.G Francisco J. Cobos Prior
