1. Activación de paquetes requeridos y creación de funciones

A continuación se enlistan los diferentes paquetes que se requieren para crear y ejecutar las múltiples funciones descritas en el manuscrito.

library(readxl)    #paquete para importar archivos con extensión *.xlsx
library(plot3D)    #paquete para la creación de figuras tridimensionales
library(zoo)       #paquete para aplicar función sobre bloques de valores

2. Creación de funciones no incluidas en R

closeness<-function(x,y,n,x_obj,y_obj){
  d<-NA
  for (i in 1:n){
    d[i]<- (((x[i]-x_obj)^2  + (y[i]-y_obj)^2)^0.5)}
  print(d)
}

distancia<-function(x,y,n){
  d<-NA
  for (i in 1:n){
    d[i]<- (((x[i]-x[i+1])^2  + (y[i]-y[i+1])^2)^0.5)}
  print(d)
}

velocidad.neta<-function(x){
  en.movimiento<-0;n<-length(x)-1
  for (i in 1:n){
    if (x[i]>0){
      en.movimiento<-en.movimiento + .2
    }
  }  
  print((sum(x,na.rm = T)/100)/en.movimiento)
}

posiciones<-function(x,y,inicios){
  equis<-0;ye<-0
  for (i in inicios){
    equis[i]<-x[i]
    ye[i]<-y[i]
  }
  print(data.frame(na.exclude(equis),na.exclude(ye)))
}

coord.X<-function(x,n){
  coord<-NA
  for (i in 1:n){
    if (x[i]==1 | x[i]==5){
      coord[i]<-46} 
    if (x[i]==2 | x[i]==6){
      coord[i]<-0}
    if (x[i]==3 | x[i]==7){
      coord[i]<-46}
    if (x[i]==4 | x[i]==8){
      coord[i]<-92} 
  } 
  print(coord)
}

coord.Y<-function(x,n){
  coord<-NA
  for (i in 1:n){
    if (x[i]==1 | x[i]==5){
      coord[i]<-0} 
    if (x[i]==2 | x[i]==6){
      coord[i]<-46}
    if (x[i]==3 | x[i]==7){
      coord[i]<-92}
    if (x[i]==4 | x[i]==8){
      coord[i]<-46} 
  } 
  print(coord)
}

3. Importación de datos

Antes de aplicar las funciones creadas, así como las que están incluidas en los paquetes activados, se deben importar los datos al entorno de R para entonces aplicar las diferentes funciones descritas en el manuscrito y producir así las representaciones de las medidas molares. En este caso se ejemplifica la forma de hacerlo desde un archivo de Excel que contiene dos hojas, una con los datos del desplazamiento en coordenadas X-Y a través de 80 sesiones y otra que contiene los datos correspondientes a lo registrado mediante el programa MED-PC, igualmente a través de las 80 sesiones de exposición al procedimiento.

## [1] "XY<- read_excel('ruta...  /Base_analisis_molar.xlsx', sheet = 'etho',na='-')"

## [1] "med<- read_excel('ruta...  /Base_analisis_molar.xlsx', sheet = 'med',na='-')"

4. Direccionalidad

Para representar la direccionalidad de manera bidimensional se emplea la función plot(), en la que se deben especificar los argumentos que se refieren a las variables que designan la posición del organismo en coordenadas X-Y. Otros argumentos empleados son: type, para especificar que los datos se representen como una línea; main, para escribir un título de la figura (si es que hace falta); xlab y ylab, para escribir los rótulos de cada eje; xlim y ylim, para especificar el rango de los ejes. Las funciones points() y text(), cumplen la función de agregar elementos en la gráfica. La primera función señala las coordenadas en las que se agrega un cuadrado (pch=0), con el doble de tamaño respecto al estándar (cex=2). La segunda función señala las coordenadas en las que se agrega uno de cuatro nombres (D1 a D4) en negritas (font=2)para identificar a cada dispensador de agua.

par(pty="s") # con este parámetro se establece un plano X-Y cuadrado 
plot(XY$X60,XY$Y60,type="l",main="Condición EC-TC (D2)",xlab="Eje X",ylab="Eje Y",
     xlim=c(0,92),ylim=c(0,92))
points(c(46,92,46,0),c(0,46,92,46),pch=0,cex=2)
text(c(46,92,46,0),c(0,46,92,46),c("D1","D4","D3","D2"),cex = 0.7,font = 2)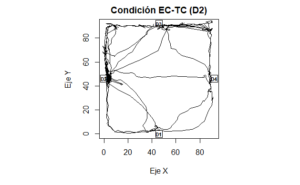

Para representar la direccionalidad de manera tridimensional se emplea la función scatter3D(), en la que se deben especificar los argumentos que se refieren a las variables que designan la posición del organismo en coordenadas X-Y, así como la variable que señala el paso del tiempo (Eje Z). Otros argumentos empleados son: colvar=, el cual es importante que se establezca como NULL para la serie de datos se muestre en un solo color (negro, por defecto); zlab, para escribir los rótulos del Eje Z. La función text3D() es útil para crear gráficos tridimensionales en los que los datos que se muestran son conjuntos de palabras, aunque en el presente código se usan para señalar las coordenadas X-Y-Z, en las que añaden (add=TRUE) las etiquetas que identifican a cada dispensador de agua.

scatter3D(XY$X60,XY$Y60,XY$Time,type="l",colvar=NULL,zlab="Tiempo",main="Condición EC-TC (D2)")
text3D(c(46,92,46,0),c(0,46,92,46),c(0,0,2159.8,2159.8),labels=c("D1","D4","D3","D2"),add = TRUE)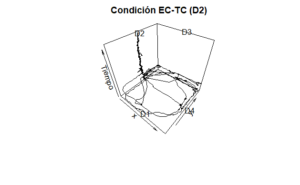

5. Cercanía-lejanía

Para representar la cercanía-lejanía se aplica la función closeness(x,y,n,x_obj,y_obj), en la que deben especificarse los argumentos que se refieren a la posición del organismo momento a momento en las coordenadas X-Y, así como a las coordenadas de la ubicación de los objetos de estímulo x_obj y y_obj y n se refiere al número de frames en el conjunto de datos. En el presente ejemplo se aplicó cuatro veces la función, debido a que había cuatro dispensadores respecto de los cuales podría juzgarce la cercanía-lejanía del organismo.

Para producir la figura que muestra las distancias calculadas se emplea el comando plot() en el que se incluyen la variable que señala el paso del tiempo (XY$Time), la distancia respecto al Dispensador 1 (d1_s60), la indicación de que la serie de datos se muestre como una línea, el tipo de línea (continua, lty=1) y el color de ésta (negra, en código hexadecimal). En las siguientes tres líneas de comandos se emplea la función points() para añadir cada una de las series de datos correspondientes a la cercanía-lejanía respecto a los Dispensadores 2, 3 y 4, respectivamente. En cada una de esas líneas se emplean los mismos argumentos que en la línea anterior, con la diferencia de que se especifica la serie de datos correspondientes, así como un tipo de línea y color diferente para cada serie. La última línea de comandos permite añadir la leyenda para las series de datos mediante la función legend().

d1_s60<-closeness(XY$X60,XY$Y60,10800,46,0)
d2_s60<-closeness(XY$X60,XY$Y60,10800,0,46)
d3_s60<-closeness(XY$X60,XY$Y60,10800,46,92)
d4_s60<-closeness(XY$X60,XY$Y60,10800,92,46)
plot(XY$Time,d1_s60,type="l",main="Condición EC-TC (D2)",lty=1,col="#000000",
     xlab="Tiempo de la sesión (en frames de 0.2 s)",ylab="Distancia Rata-Dispensador (cm)")
points(XY$Time,d2_s60,type="l",lty=2,col="#333333")
points(XY$Time,d3_s60,type="l",lty=3,col="#666666")
points(XY$Time,d4_s60,type="l",lty=4,col="#999999")
legend("bottomright" , inset=c(0,1),cex=0.8,horiz=T,
       legend = c("D1", "D2","D3","D4"), xpd=T,lty=c(1,2,3,4),bty = "n",
       col = c("#000000","#333333","#666666","#999999"))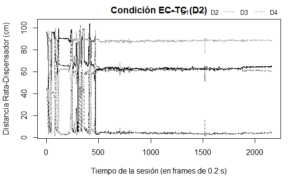

6. Vigor

Para representar el vigor se debe aplicar la función distancia() para obtener el cálculo de la distancia recorrida frame a frame. Para graficar el dato es suficiente con usar la función plot(), en la que se señala el paso del tiempo como la variable que establece los datos de las abcisas y el resultado obtenido de la distancia recorrida como la variable para las ordenadas. Ésta última variable debe ir incluida dentro de la función cumsum() para que se muestre la distancia recorrida acumulada a través del tiempo. Se añade con la función text() la descripción de la distancia total recorrida, obtenida mediante la función sum(), así como la velocidad neta, obtenida mediante la función velocidad.neta().

dist_s60<-distancia(XY$X60,XY$Y60,10800)
plot(XY$Time,cumsum(dist_s60)/100,type="l",main="Condición EC-TC (D2)",ylim=c(0,80),
     xlab="Tiempo de la sesión (en frames de 0.2 s)",ylab="Distancia recorrida (metros)")
text(0,60,adj = 0,paste("DT = ", format(sum(dist_s60,na.rm = T)/100,digits = 4),"m"))
text(0,50,adj = 0,paste("VN = ", format(velocidad.neta(dist_s60),digits = 4),"m/s"))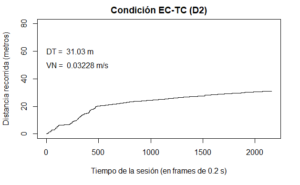

7. Preferencia

Para representar la preferencia (como el tiempo acumulado en las diferentes áreas del espacio experimental) es suficiente con emplear la función hist3D(z), la cual también se encuentra incluida en el paquete plot3D y donde z se refiere a una tabla conformada por un número de renglones y columnas en las que se distribuye el conteo de visitas. Para crear dicha tabla sólo se requiere emplear la función cut(x,n) para segmentar la variable x (así como la variable y) en n intervalos, para posteriormente crear la tabla necesaria mediante la función table().

En el presente ejemplo se ilustra la segmentación del área experimental en 100 áreas (10 x 10). Debido que lo que se obtiene como resultado es el número de veces que se visitó cada área, este dato (z60)se multiplica por 0.2 para transformarlo a tiempo (en virtud de que la duración de cada frame es de 0.2 s). En la función hist3D() es posible emplear los mismos argumentos que se describieron para la función scatter3D(). Algunos otros argumentos, como los que se incluyen en este ejemplo, sirven para establecer que los ejes X, Y y Z contengan información precisa de su segmentación (ticktype=“detailed”), que se marquen las aristas de cada barra en color negro (border=“black”), que se muestre un tipo de fondo gris (bty=“g”) y que la orientación angular del cubo sobre su eje horizontal (phi=20).

x60<-cut(XY$X60,10)
y60<-cut(XY$Y60,10)
z60=table(x60,y60)

hist3D(z=z60*.2,colvar = NULL,col="gray",ticktype = "detailed",
       border="black",zlim=c(0,1500),bty = "g", phi = 20,
       xlab = "D1", ylab = "D4", zlab = "",cex.axis=0.7,
       main="Condición EC-TC (D2)")
text3D(c(0.5,0),c(1,0.5),c(1400,1400),labels=c("D3","D2"),add = T)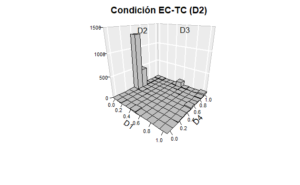

8. Variación

Para representar la variación se calculó la diferencia entre la distancia recorrida en cada ciclo y la trayectoria ideal (en términos de la ruta más corta entre la ubicación inicial del organismo y la ubicación del objeto de estímulo al final del ciclo). Para calcular la distancia recorrida en la ruta seguida en cada ciclo se emplea la función rollapply(), del paquete zoo, en la que se especifica que la variable que contiene las distancias recorridas frame a frame (i.e., dist_s60, calculada previamente) será dividida en segmentos de 150 valores (width=150), se establece que se han de sumar todos los valores de cada segmento generado (FUN=sum, by=150).

En cuanto al cálculo de las distancias implicadas en las trayectorias ideales desde la posición del organismo al inicio de cada ciclo y la ubicación del objeto de estímulo al final de cada uno de éstos, primero se genera una variable en la que cada valor corresponde al número de frame en el que inicia cada ciclo (inicios). Posteriormente se obtienen las coordenadas de la ubicación al inicio de cada ciclo mediante la función posiciones(), en la que se utiliza la variable generada inmediatamente antes. Es importante destacar que al aplicar la función posiciones(), el resultado es filtrado mediante la función na.omit() para suprimir todos los valores que no corresponden a los inicios de cada ciclo (es decir, todos los valores intermedios). Mediante la aplicación de la Ecuación 1 (véase el manuscrito) se obtiene la estimación de la distancia de cada trayectoria y, finalmente, se calcula el valor absoluto de la diferencia entre cada trayectoria ideal y la ruta de desplazamiento para obtener la distribución de tales diferencias como un indicador de la variación. En el ejemplo mostrado se emplea la función boxplot() para graficar la distribución de las diferencias entre trayectorias y ruta por ciclo. La función axis() permite señalar que en el eje de las abcisas (1), en la posición número 1 se habrá de colocar la etiqueta correspondiente para la gráfica de caja y cejas que se proyecta (labels=c(“Condición EC-TC”)). El segundo y tercer argumento pueden admitir una lista de valores y etiquetas, respectivamente, en el caso de que se incluya más de una gráfica en el plano (como en el manuscrito).

ruta.pc60<-rollapply(c(0,dist_s60), width=150, FUN=sum, by=150)

inicios<-seq(1,10800,150)

pos60<-na.omit(posiciones(XY$X60,XY$Y60,inicios))

traj.pc60<-sqrt((pos60$na.exclude.equis.-0)^2 + (pos60$na.exclude.ye.-46)^2)
var60<-abs(ruta.pc60-traj.pc60)/100


boxplot(var60,main="",xaxt="n",ylab="Diferencia entre ruta y trayectoria (mts)")
axis(1,at=c(1),labels=c("Condición EC-TC"))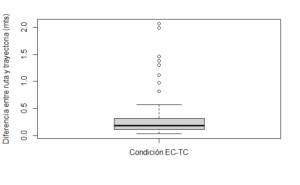

9. Persistencia

Para representar la persistencia es suficiente con graficar el dato recolectado por el software en el que se programó la tarea experimental. En este caso, el registro realizado mediante MED-PC de las entradas a cada dispensador. En particular, para el experimento que se describe en el manuscrito se calculó la suma de entradas a cada dispensador, registradas en los subintervalos de tiempo en los que no había disponibilidad de agua. Mediante la función de concatenación (c()) se incluyeron las cuatro cantidades totales en una sola variable (*entradas_s60) y se graficaron con la función barplot() como un gráfico de barras.

Es importante destacar que en cada experimento podría variar la manera en la que se registran las respuestas persistentes del organismo, pero independientemente de eso el modo de representación es muy sencillo y directo una vez que se cuentan con las frecuencias totales.

ent1.s60 <-med$B1_S60[21736:21762]
ent2.s60 <-med$B2_S60[21736:21762]
ent3.s60 <-med$B3_S60[21736:21762]
ent4.s60 <-med$B4_S60[21736:21762]

entradas.s60<-c(sum(ent1.s60),sum(ent2.s60),sum(ent3.s60),sum(ent4.s60))
barplot(entradas.s60,names.arg = c("D1","D2","D3","D4"), axis.lty = 1,
        main = "Condición EC-TC (D2)",ylim = c(0,250),xlab="Dispensadores disponibles", 
        ylab="Frecuencia de re-entradas")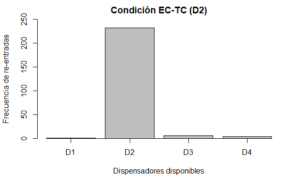

10. Referencias

Ribes-Iñesta, E. (2007). Estados y límites del campo, medios de contacto y análisis molar del comportamiento: reflexiones teóricas. Acta Comportamentalia: Revista latina de análisis del comportamiento, 15(2), 229–259.

Soetaert, K. (2019). plot3D: Plotting Multi-Dimensional Data. R package version 1.3. https://CRAN.R-project.org/package=plot3D

Wickham, H. & Bryan, J. (2019). readxl: Read Excel Files. R package version 1.3.1. https://CRAN.R-project.org/package=readxl

Zeileis, A.& Grothendieck, G. (2005). zoo: S3 Infrastructure for Regular and Irregular Time Series. Journal of Statistical Software, 14(6), 1-27. doi:10.18637/jss.v014.i06